Het vak wiskunde kan worden opgedeeld in verschillende domeinen: meetkunde, rekenen, verbanden en statistiek. Die opdeling geeft overzicht in een vak dat heel breed is en een eindeloze reeks aan formules kent. Toch hebben de verschillende domeinen met elkaar te maken. Soms is het nodig om eens een wiskundige bezigheid te hebben waardoor de samenhang zichtbaar wordt. Niet alleen de samenhang tussen de domeinen in de wiskunde, maar ook tussen wiskunde en natuur- en scheikunde en kunst.

Sneeuw

In de koude week van 8 februari, gingen de leerlingen met een maatbeker de straat op en schepten die vol met sneeuw. Die sneeuw lieten ze binnen smelten en met de rekenregels voor procenten, kwamen we erachter dat er meestal wel 60% of 70% van het volume verdwijnt als de sneeuw smelt. Met die kennis konden we ook een goede schatting maken van het gewicht van de sneeuw die op een tuintafel was gevallen.

Maatbekers met sneeuw, voor en na het smelten

Dat zo een groot deel van het volume van de sneeuw verdwijnt als het smelt, konden we verklaren met de natuurkundige en scheikundige eigenschappen van water, waar sneeuw uit bestaat. Water zet uit als het bevriest, maar belangrijker is nog wel dat sneeuwvlokken een zesvoudige symmetrie krijgen door de vorm van de H20-moleculen van het water. Die kenmerkende eigenschap van de moleculen, konden we vertalen naar meetkunde en die konden we gebruiken om de mooie patronen van sneeuwvlokken te begrijpen en na te maken met papier.

Sneeuwvlokken van papier gemaakt (Hoe kun je mooie sneeuwvlokken knippen die zesvoudige symmetrie hebben?)

Spiralen

In de warme week van 15 februari ontdekten de leerlingen hoe een getallenrij zorgt voor spiralen in de natuur (slakkenhuisjes, patronen in zonnebloemen).

Het gaat hier om de getallen van Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, ...

Steeds als je de twee laatste getallen bij elkaar optelt, krijg je het volgende getal in de rij. Die getallen kun je weergeven als vierkanten die samen een spiraal vormen. Dat is te zien op de eerste tekening van een leerlinge van klas x3j.

Deze spiraal komt op veel plekken in de natuur terug. Huisjes van slakken, de schubben van een dennenappel, de harten van bloemen volgen allemaal deze spiraalvorm. Helemaal opvallend is het dat de aantallen spiralen altijd twee opeenvolgende getallen van de getallenrij van Fibonacci zijn!

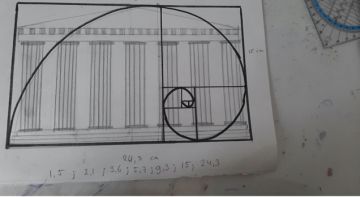
De getallenrij van Fibonacci kan worden weergegeven als een spiraal van vierkanten

De rechthoek waar de spiraal doorheen draait, voldoet aan de zogenaamde Gulden Snede, die veel in de kunst en architectuur gebruikt wordt. Deze verhouding tussen lengte en breedte geeft een evenwichtig en mooi beeld. Als afsluitende creatieve opdracht, ontwierpen de leerlingen een eigen gebouw gebaseerd op de getallenrij, de spiraal en de gulden snede.

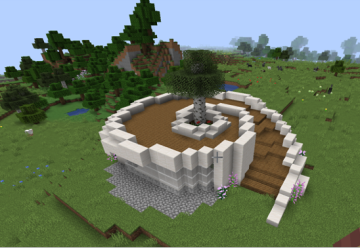
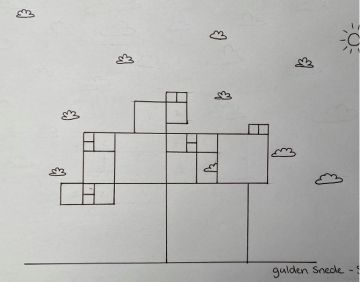
Bouwwerken gebaseerd op de gulden snede, ontworpen door de leerlingen van 3 havo